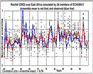
We now have one estimate of the seasonal climate for each season, given the SST that was prevailing in that season. However, as discussed above, there is always a battle between the SST controlling the seasonal climate, and other factors internal to the model. To allow us to study this battle, 23 further runs of the model were made. The only difference is that each run starts from a different January weather pattern. This allows us to see the extent to which, in each season, the model's climate anomalies are being determined by the prevailing SST anomalies, versus the extent to which the model is able to ignore the prevailing SST anomalies and create a range of climate anomalies in each of the 24 runs. To illustrate this, we take the models simulated rainfall in East Africa. We average the rainfall simulated by the model in each October-December rainfall season. To study the climate anomalies, we subtract the mean model rainfall over all 24 runs and over all years, and express each model seasonal rainfall total as the number of standard deviations above or below the average rainfall simulated by the model. The standardized rainfall anomaly simulated by the model for each season by each of the 24 runs is shown in Fig. 2.2. Consider the year 1997. Each time the model ran through the October- December season for 1997, it was feeling the SST anomalies that prevailed during that season, a very strong El Niño pattern, along with anomalously warm SST in the western Indian Ocean. In 23 out of 24 of the model runs, the model simulated rainfall above average. Thus, the prevailing SST anomalies in 1997 seem to be quite strongly pushing the model toward producing above normal precipitation, but still, the model has a degree of independence from the SST (indeed, one of the 24 runs actually simulated below normal rainfall, as seen on Fig. 2.2). The 24 values can be viewed as the model's estimate of the range of rainfall conditions possible given the SST forcing. The average of the 24 runs can be considered the model's best estimate of the mean rainfall to expect given the prevailing SST conditions. It can be considered as the best estimate forecast the model would make for 1997, based on knowledge of the SST prevailing through that season. For 1997, that forecast would have been very accurate for the area-average rainfall. The red line in Fig. 2.2 shows the average of the 24 model runs and the blue line shows the observed standardized rainfall anomaly in each year. It can be seen that the model has good ability to anticipate the observed rainfall anomaly, given the prevailing SST anomaly (correlation between best-estimate prediction and the observed is 0.74). It is certainly better than rolling a dice. Such levels of skill are found in only a few tropical regions. Away from the tropics and the Pacific region, it is difficult to identify skill for many regions. Fig. 2.3 illustrates how the plot looks for such a region. It should be emphasized that some GCMs are better in certain regions than others (see discussion in lecture 3 of the optimum approach of combining the predictions from many different models). Conclusions of absence of skill should not be drawn based on the results of one GCM alone.