Statistical Transformation of Dynamical Model Output

As referred to in lecture 3, output from GCMs and RCMs usually benefits from at least some statistical correction. Here we go beyond simple statistical transformation of the mean and variance (for example, the mean bias correction in Fig. 3.5). The forecast fields generated by the climate models are now treated as statistical predictors for the information that is needed. This section reviews some of the statistical techniques that are being tried. Some of these could also be applied in the direct statistical approach discussed at the beginning of this lecture and illustrated by the example of predicting stream-flow from sea-surface temperature indices (Fig. 4.1). Now, by using output from the GCMs or RCMs as predictors, the requirement of identifying physically realistic predictors is made somewhat simpler, but not removed. The analyst should still diagnose the source of large scale predictability in the GCM (for example, as demonstrated for East Africa in lecture 2) before using the large-scale fields as predictors for downscaled information. The approach is often referred to as statistical downscaling of global climate model output. In global change research, it is often referred to simply as statistical downscaling.

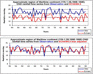
To illustrate the problem of downscaling to the seasonal rainfall total at an individual station, the example of a station in East Africa is used. First, the rainfall predicted by the nearest GCM grid-point is considered (Fig. 4.11a). Any bias in mean or variance could be corrected as previously discussed (simple model output transformation, e.g. Fig. 3.5), but this would not improve the correlation skill score. It is likely that the individual grid-point predicted by the GCM is rather noisy (influenced by random weather events generated by the model during the season). Furthermore, it is also likely that the GCM makes a spatial shift in its prediction for this point (that is, the model correctly responds to the prevailing SST pattern and increases rainfall in the general region, but repeatedly places the increase in rainfall in the wrong location). Both of these factors suggest that there should usually be better information in the large-scale GCM prediction. A first step could be to treat the rainfall anomaly predicted across the region as the predictor for the individual station. Here, we use the GCM regional index calculated in the practical exercise of lecture 2 as the predictor:

R = -566.392 + 8.31 (Rreg) ..........Eq (1)

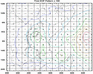
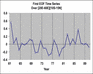
Applying this approach in cross-validation mode yields predictions with a correlation skill of 0.64, so some increase in skill is found in this example. Further information may be possible from the broader large-scale fields in the GCM. The GCM may systematically shift the pattern of rainfall anomalies associated with a forcing like the SSTs of an El Niño event . How to create an index of the broad pattern predicted by the GCM in each year? We can imagine that a weighted average across a broad domain, placing most weight where the model shows most tendency to coherently increase or decrease rainfall from year-to-year, could be a good choice. Principal component analysis (PCA) is a commonly used statistical tool that can provide us with such an index. Fig. 4.11b shows the first Principal component weighting pattern for the mode's predicted rainfall over East Africa and the western Indian Ocean. It can be seen that most weight is being placed over the ocean. The first principal component time-series (Fig. 4.11c) is a weighted average of the rainfall predicted across the PC domain, weighting according to the values in the PC pattern. Thus, when we use the first PC timeseries as a statistical predictor for the station, we are effectively giving more weight to the rainfall predicted over the ocean and less weight to that predicted over land.

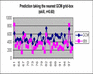
For the Kenya station example, using the first PC to predict the rainfall gives a prediction relationship:

R = -5.475 + 1.019 (PC1) ..........Eq (2)

Applying this approach in cross-validation mode yields the predictions shown in Fig. 4.11d. The correlation skill shows a modest further increase in this situation. In other locations, the increase in skill is being found to be more substantial. It is also possible to extend the principal component domain, including predicted GCM fields in known key forcing areas for the climate of the target region, such as the Equatorial western Pacific.

Most regression-based methods produce predictions with a variance that is less than the observed. Most widely available methods use the least-squares error principle to fit model parameters. In such situations, to transform the predicted series into one with the same variance as the observed, the predicted anomaly is multiplied by (1/r), where r is the correlation skill of the model fit (for this adjustment, the prediction series must be transformed into anomalies with zero mean over the analysis period).

Making such an analysis for one station/location in isolation is not good practice. There is a need to place the skill for the target station in the context of broader regional downscaled predictability, to gain confidence that the result is robust. Fig. 4.12 shows statistical downscaled skill applying the method in Equation 2. A dense network of stations has here been gridded at 20kmx20km resolution. Forecasts are made for each individual grid-box and the correlation skill calculated for each grid-box. The correlation skill score is then contoured to make the map shown in Fig. 4.12. The results suggest that skill is substantial on the eastern side of the island, but generally poor in western and southwestern parts. One hypothesis is that a mechanism like that indicated in Fig. 4.2 is operating, since indeed, generally wetter years are associated with stronger easterly winds across Sri Lanka, which could enhance precipitation on the windward side of the island, but with some compensation in the lee of the mountains, meaning precipitation there is not so clearly impacted by the predictable winds. Such results with statistical downscaling can therefore lead to a hypothesis that can be tested using dynamical downscaling with physical climate models. This combination of analysis methods can enhance confidence in downscaled information for use in sectoral applications such as in agriculture and water resource management.