(v) Statistical Methods

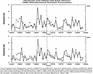
Statistical methods have the advantage that they require minimal computing power, whereas for the General Circulation Models, some of the world's most powerful computers are needed. Statistical methods usually employ one or more predictors to forecast a target variable, which is often referred to as the predictand. A simple example of a statistical forecast method is a linear regression that uses one or more SST indices to predict a seasonal rainfall index. Fig. 3.6 gives an example of forecasting a regional rainfall index for East Africa using three SST indices as predictors. In this case, the predictors are three indices of SST, that were generated objectively by applying an empirical orthogonal function (EOF) analysis to the global SST dataset. More complex multivariate methods such as canonical correlation analysis have also been applied, and models have also been successfully used to forecast SST, especially indices of el niño. The statistical methods can also be designed to provide probability estimates of different outcomes.

While statistical methods may in many locations currently be able to perform in real-time at comparable levels to GCMs, there is a critical problem of choosing the appropriate predictors for the models. There are a very large set of candidate predictors that can be considered, even if one restricts the choice to aspects of the global SST field. There is ever present the risk of finding a good match between a predictor index and the predictand, when in fact the match is partly or wholly the result of a statistical fluke over the years for which data are available. Methods like cross-validation and retroactive forecasting, or testing of models on independent periods, all help in assessing the expected real-time performance of statistical methods, but it is still possible to search enough candidate predictors to generate skill on past data where no physical basis exists, or to inflate the skill substantially by finding alternate predictors that co-vary with the true forcing factor. This is particularly true of predictors that co-vary with el niño. Consider, for example, that your predictand has a correlation 0.4 with Nino3, and this is physically well founded. There are many variables in the climate system that co-vary with Nino3 - for example, you may search through 10 such variables in the hope of finding a better predictor than Nino3. Let us considered that all these variables have a Nino3 signal and a random noise component. On average, for half of these new candidate predictors, the noise component will further contribute to the correlation with your predictand, while in the other half, the noise component will reduce the correlation with your predictand. It is likely that for at least one of the candidate set, the noise will, by statistical fluke, quite substantially inflate the correlation with your predictand. However, there is no basis for assuming this predictor will perform better than Nino3 in the future. Indeed, it likely will perform worse, since it only partly covaries with the true physical forcing factor, in this case assumed to be Nino3. This example is intended to illustrate the difficulty of selecting predictors in a way that avoids artificial skill - especially artificial skill that arises due to the selection predictors from a large candidate set, whether the predictors are selected objectively or subjectively. Another form of artificial skill arises if we make forecasts for a very large set of predictands. We may select predictors in a very objective way, but we know that some of the predictands will appear to be predictable just by chance. This form of artificial skill is also present when numerical models are validated over many grid-boxes, as discussed in lecture 2, when it was emphasized that even for GCM forecasts, the need for physical explanations of predictability is important.

Thus, at the root, for statistical prediction, is establishing that the statistical relationships are reflecting real physical processes in the climate system. A particularly difficult issue is the potential use of atmospheric predictors. As discussed in the introduction to this lecture, there are possible ways in which the atmosphere (including in the stratosphere) could impact the seasonal evolution of climate, such that adding them as predictors into a statistical scheme could provide a genuine contribution to accuracy of the seasonal prediction scheme. However, the scientific uncertainty surrounding such alternate sources of predictability deters their use in most current operational systems.

There is a further twist to the potential use of atmospheric predictors in statistical seasonal prediction schemes. It could be argued that the current and recent atmospheric patterns could provide a clarification of the mix of prevailing SST forcing for the region of interest, and thereby provide additional predictor information above any individual SST index or combination of a few indices. However, such alternate atmospheric-based predictors need to be carefully evaluated to ensure they are genuinely reflecting SST-forcing. Modelling studies could potentially establish such a basis.

Statistical methods may be able to make a more immediate and clearer contribution when the predictors are clearly established SST indices that have been shown to be associated with large-scale atmospheric circulation in the target region. The way to begin to approach this was demonstrated in the types of analysis illustrated in Fig. 1.10.