The above discussion has considered these methods in the context of generating meteorological variables. They could also be applied directly to the information of interest such as stream flow. For example, Landman et al 2001 use the perfect prognosis regression-based approach for seasonal stream flow at sites is South Africa. However, if the statistical techniques are used to generate meteorological variables, there is often a need to evaluate the consequences of this meteorological prediction. Examples would include driving hydrological models with daily weather to predict the statistics of daily stream flow, driving environmental models that predict variable of key importance for diseases, such as mosquito distributions, and driving crop models with daily sequences of weather to predict crop production under various assumptions.

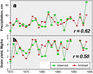
Figure 4.14 gives an example of such an application using output from an earlier version of the ECHAM GCM to predict maize yield at a case study site in Kenya. In this example, the crop model is driven with daily weather sequences created using a weather generator conditioned on the mean prediction of the ECHAM GCM for the region in each year (the GCM prediction experiment used time varying observed SST, as described in Part 2). For comparison, the crop model is driven with the actual observed daily weather features in each season - giving an estimate of the crop production that would have occurred in each year, given the actual observed weather. The match of the two time-series indicates that the seasonal prediction of crop yield compares reasonably well with the crop yield that is given for the actual observed climate conditions in each season. The accuracy of the crop yield prediction (correlation skill 0.50) is only moderately reduced from the accuracy of the seasonal prediction for the seasonal rainfall total (correlation skill 0.62).

Many more tests like this are needed to establish the relative predictability of seasonal rainfall and consequences of the climate, like crop production. Furthermore, there is a need to test the range of methodologies that are possible for arriving at the downscaled meteorological information that creates the crop yield prediction. Regardless of the optimum methodology, emerging evidence here and elsewhere supports the cascade of large-scale prediction skill into the features that impact agriculture and other socially relevant weather-impacted features, like stream flows and mosquito distributions. Thus, the creation of decision support using the best currently available information is an issue for today.

Decision Support

Research results like that in Fig. 4.14 are a step toward providing better guidance for decision-making. However, the best decision support is created through integrating information with the decisions themselves. For the example in Fig. 4.14, one could consider the decision options available at the farm level, and evaluate each of those options over past years, under different response strategies to the seasonal prediction information. For example, Messina et al. (1999) consider decisions about land allocation to different crops under seasonal prediction information.

With such complex systems into which climate information is being injected, the best decision support is usually not considered to be of a single prescriptive type. One approach makes quantitative analyses of different strategies under different assumptions. The analyses run for situations in past years when the seasonal forecast and actual outcomes are known. This allows the expected average net benefit to be estimated for different response strategies to seasonal forecasts, along with the year-to-year variation in the consequences of given response strategies. Information on the year-to-year variation in the consequences is important because it is possible for a net benefit to be achieved, but for the costs in a small number of years to be unacceptable. In a real-time setting, these analyses allow estimation of the consequences of a range of responses, conditioned on the range of possible climate outcomes indicated by the seasonal prediction. It can be desirable for the user to be able to manipulate the scenarios themselves. There are other types of tools that can also form decision support, the aim being to provide information that places the decision-maker in a more informed environment in which to evaluate their response to the climate information, and to combine this with other factors, for which decision support tools may already exist and indeed which may be adapted to include new forms of climate information. Decision support is a complex subject in its own right, partly drawing on decision and cognitive sciences, and with particular challenges in this setting due to the probabilistic nature of seasonal predictions. This section is therefore but a pointer to the many challenges of providing decision support. It is however a key aspect of integration into society for complex scientific information like downscaled seasonal forecasts.