Limits to a purely statistical approach

However, for most of the downscaled features of interest, new knowledge is needed on Requirement 2 above, that is, the cascade of predictability from the large scale circulation to the feature of interest. An example is if we wish to make forecasts for individual point locations, such as represented by rainfall stations. We may identify a predictor that has good physical basis for influencing the large-scale rainfall across a region. When we come to calculate the skill of the statistical predictor for each individual station, we will necessarily see variations in the level of skill simply due to the small sample size we have available to us in the historical record (perhaps typically about 30 years, giving 30 pairs of value to correlate). In contrast, consider a situation where we have a very long time series of reliable observed data, say 2000 years. And consider that, in this situation, the relationship between the SST predictor and the rainfall at each station is in fact exactly the same (at a correlation level of 0.4) - and with 2000 years to sample the relationship, each station does indeed show a near exact correlation of 0.4 with the SST predictor. However, if we just take a sample of 30 years from the record, because of the small sample size and the random noise in the time-series of each rainfall station, the correlation with each rainfall station can vary quite substantially: some sampled correlations may well be lower than 0.3 and others higher than 0.5. Yet in this situation, if we tried to make forecasts of varying confidence for the stations, based on the sampled relationship with the predictor over the 30 year period, we would degrade the forecast system - since the station that appears to have high predictability in the 30 years sampled will not, in the long run, have any higher predictability than the other stations. The best strategy would have been to assume all stations have the same strength of relationship with the predictor. Indeed this can be considered the first order approach to generating high resolution predictions - that is - to assume the same anomaly forecast over the target region. In such a situation, if high resolution forecasts of actual rainfall amounts are needed, these could be generated by adding this anomaly to the spatially varying background climatology.

The need for physical understanding

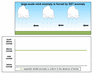
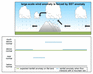
Thus, when we are actually trying to make advances in understanding of predictability in order to do downscaling, we will often need to resort to physical understanding in order to justify spatial details in the downscaled forecast anomaly information. For example, Figure 4.2a-b provides an example of a physical process that could provide the basis for detailed spatial downscaling. Assume that, for the region in Fig. 4.2, SST forcing (e.g. associated with El Niño) tends to induce anomalous easterly winds (as shown in Fig. 4.2a), which in turn tend to favour above normal rainfall across the region. However, if there is a substantial chain of mountains in the region, the anomalous easterly wind may interact with the mountains to create a fine structure to the rainfall anomaly pattern. For example, this could make the windward side of the mountains particularly favourable for even more greatly enhanced rainfall, at the expense of the leeward side (as schematically illustrated in Fig. 4.2b).

This is a very simple illustration and the mechanisms in the real atmosphere will be more complex. However, the example is illustrative of the concept. In this situation, when the SST favours anomalous easterly wind, rainfall is particularly enhanced in a sub-region (the windward side of the mountains), such that we would expect a higher correlation between the seasonal rainfall total here and the SST index when calculated over many years, relative to the lee side. In an extreme situation, the correlation may actually be of opposite sign in a small pocket on the lee side of the mountain - that is, while the anomalous easterly wind is generally favourable for above average rainfall over the region, the particular enhancement on the windward side of the mountain actually results in a compensation on the lee side of the mountain so that this pocket actually tends to receive below normal rainfall. A time series of rainfall for this small pocket on the lee side of the mountain and the SST index would then have a correlation with a sign that is opposite to that for the rest of the region. The problem we have is to know whether such mechanisms are operating and creating a basis for making contrasting forecasts of small-scale rainfall anomalies within a larger region. Analysis of simulations by climate models can provide insights to this problem. Using numerical climate models to investigate and generate the high resolution information is commonly termed dynamical downscaling.

Dynamical Downscaling

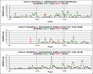
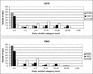
As a first evaluation, we might consider the ability of GCMs to simulate the spatial rainfall variations and temporal features such as dry spells and storms. However, we do not anticipate much success with the raw output from the GCMs because of their course horizontal resolution (typically about 250km grid-point spacing). The typical spatial scale of a GCM was illustrated in Fig. 3.4. As an example, the GCM is evaluated for two contrasting years in this region - 1975 (unusually wet) and 1983 (unusually dry). In terms of capturing the relative difference between the two years, the GCM successfully predicts 1975 to be wetter than 1983. However, when this GCM is evaluated for its ability to simulate temporal and spatial details of rainfall over West Africa it is clearly deficient. It is unable to capture the tight north-south gradient of rainfall (Fig. 4.3). As for the daily rainfall sequences (Fig. 4.4a-b), the result is rather typical of a GCM - it fails to produce realistic spells of dry days, rather it tends to produce a lot of days with a small amount of rainfall.

We are more optimistic about being able to simulate key processes (such as interaction with orography like in Fig. 4.2 and realistic numbers of weather events and dry spells during the seasons) when climate models are run at higher resolution. Often, the ways that the model treats some of the physical processes will need to be modified when their resolution is substantially reduced. Running at resolutions typically in the range 10-50km seems to be able to yield better representation of some of the key climate processes for downscaling. We could ideally run the global models (the GCMs) at such high resolutions, but this is computationally an enormous challenge, and evidence from regional climate models (see below) indicates a need for different parameter tuning for different regional settings in order to achieve realistic results. An example of running a global model at resolutions down to about 10km is being developed at the Earth Simulator in Japan. Another research area is to develop global models with variable resolution, such that the model user can specify a target region over which the resolution should be highest.