Impact of temperature error models in a univariate
ocean data assimilation system
Michael K. Tippett 1, Ming Ji
2, Alexey
Kaplan3
Ocean data assimilation systems combine
observations with information from prediction models to produce an
analysis or estimate of the ocean state. Statistical interpolation
assimilation methods use observations to correct a model-based first
guess and require specification of first-guess and observation error
statistics. Often the first-guess error covariance (FGEC) is described
by an analytical covariance function whose structure is not directly
related to ocean dynamics. On the other hand, ensemble and
reduced-space methods represent the FGEC by a low-rank approximation
coming from the dynamical model. Here we examine the impact of adding
a low-rank FGEC component to an operational univariate ocean data
assimilation (ODA) system. Small-scale structures are eliminated from
the mean temperature correction and positive impact is seen in the
zonal currents.
The ODA system uses the MOM-1 Pacific basin model with TAO, XBT and
blended SST observations as described in (Behringer et al., 1998). At each
assimilation time, the model first-guess is compared to observations
and a temperature correction is calculated by minimizing a cost
function (Derber & Rosati, 1989). The cost function rewards, with weight
depending on the observation error covariance, temperature corrections
that reduce mismatch between analysis and
observations. Simultaneously, temperature corrections whose magnitude
and spatial structure are incompatible with the FGEC are
penalized. The spatial structure of the FGEC controls how first-guess
errors are corrected in a neighborhood of the observation, an
important property when there are few observations.
We compare a control analysis
with one obtained using a FGEC model with low-rank component.
The control analysis is produced using a FGEC model Gf with
Gaussian horizontal correlations and temperature gradient dependent
vertical correlations (Behringer et al., 1998). The reduced-space FGEC Sf
has the form
Sf = 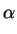 Gf Gf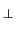 + ZFZT = + ZFZT = 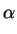 (I - ZZT)Gf(I - ZZT) + ZFZT (I - ZZT)Gf(I - ZZT) + ZFZT |
(1) |
where
0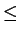
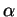
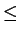 1 is a tunable parameter, the columns of the
matrix Z are the EOFs of a simulation and F is a symmetric
positive definite matrix. This formulation, like that of
Hamill & Snyder (2000) is simple to implement in an existing 3D-Var
system; in this formulation however, we assume the reduced-space and
analytical parts to be uncorrelated. For the special case
1 is a tunable parameter, the columns of the
matrix Z are the EOFs of a simulation and F is a symmetric
positive definite matrix. This formulation, like that of
Hamill & Snyder (2000) is simple to implement in an existing 3D-Var
system; in this formulation however, we assume the reduced-space and
analytical parts to be uncorrelated. For the special case 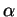 = 0
whose results are presented here, calculation of the temperature
correction is simplified. We consider the period March, 1993 -
February, 1997 and use the reduced-space spanned by the first 80 EOFs.
= 0
whose results are presented here, calculation of the temperature
correction is simplified. We consider the period March, 1993 -
February, 1997 and use the reduced-space spanned by the first 80 EOFs.
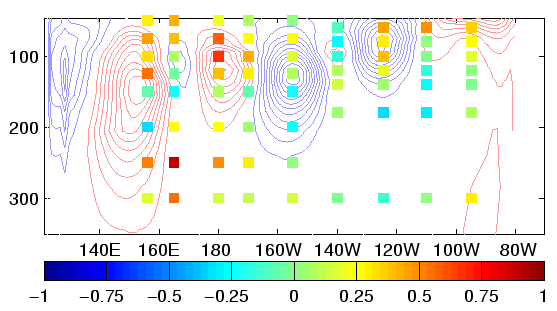
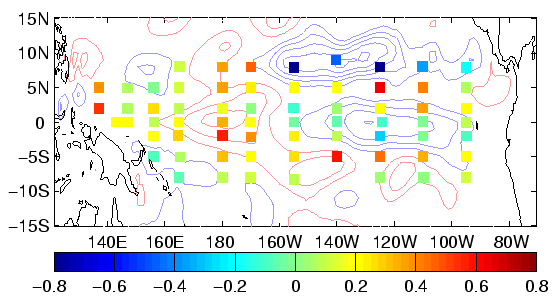
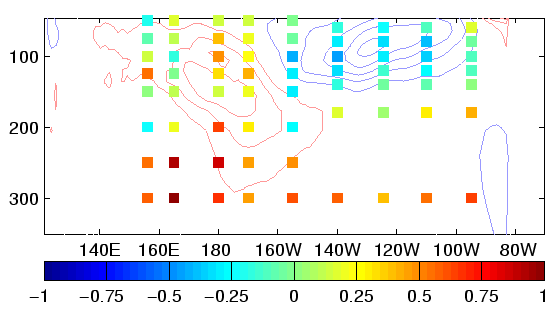
The mean temperature correction and the mean difference between
observations and analysis are significantly different from zero,
indicating systematic biases (Fig. 1). The
reduced-space analysis is generally less constrained by observations
than the control analysis. In both cases, the mean temperature
correction is correlated with the mismatch between analysis and TAO
data. In the control analysis, the mean temperature correction maxima
and minima correspond to TAO locations, producing structures with
lengthscales on the order of the TAO mooring spacing. These structures
do not appear in the analyzed temperature field or its derivatives. In
the reduced-space experiment, the mean temperature correction attempts
to correct the same model and forcing deficiencies but does so with
larger scale structures. In both experiments the impact on the
analyzed temperature fields (compared to simulation) is qualitatively
similar. However, the impacts on the zonal currents are different
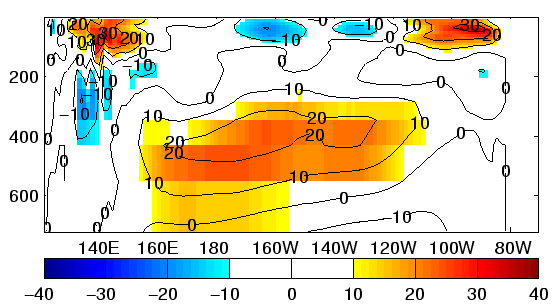
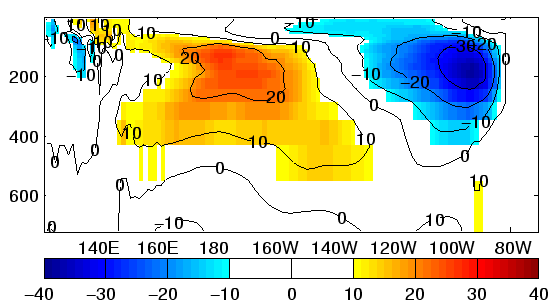
(Fig. 2). The mean zonal surface current
exceeds -50 cm/sec. in the Eastern Pacific for the control case while
the measured value at (0oN,110oW) is -17.3 cm/sec. The
equatorial undercurrent core in the control is weakened by about 12
cm/sec and shifted to the west compared to the reduced-space
experiment. Similar impacts on zonal velocity are seen when
simulations are forced with time-independent mean temperature
corrections.
Temperature error models in univariate ocean data assimilation systems
impact zonal velocity. The temperature corrections produced using a
reduced-space FGEC have less small-scale structure and were seen to
have a positive impact on zonal currents. In the reduced-space FGEC
model used here (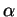 = 0), errors are reduced only on the
reduced-space which in the reduced-space Kalman filter causes
divergence (Cohn & Todling, 1996). The choice here of simulation EOFs to span
the reduced subspace is not necessarily appropriate even in the most
idealized systems since the simulation EOFs do not include the effect
of data assimilation or model error (Tippett et al., 2000).
Therefore, likely there is benefit in considering a FGEC with both
reduced and analytical parts (
= 0), errors are reduced only on the
reduced-space which in the reduced-space Kalman filter causes
divergence (Cohn & Todling, 1996). The choice here of simulation EOFs to span
the reduced subspace is not necessarily appropriate even in the most
idealized systems since the simulation EOFs do not include the effect
of data assimilation or model error (Tippett et al., 2000).
Therefore, likely there is benefit in considering a FGEC with both
reduced and analytical parts (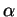 > 0). Future work will examine
impact on forecast skill.
> 0). Future work will examine
impact on forecast skill.
Figure 1:
Mean temperature corrections (positive (negative) contours
are red (blue)) and TAO observations minus analysis (colored squares)
(a) vertically averaged (50 - 500m; contour interval of 0.004oC
/ hour) and (b) along the equator (contour interval of 0.008oC /
hour)) for the control case. (c) and (d) as in (a) and (b) but for the
reduced space analysis.
(a)
 |
(b)
 |
(c)
 |
(d)
 |
|
Figure 2:
Mean difference in cm/sec of simulation equatorial zonal
currents and (a) control analysis and (b) reduced-space analysis.
(a)
 |
(b)
 |
|
-
Behringer, D. W., Ji, M. & Leetmaa, A. (
1998):
-
An improved coupled model for ENSO prediction and implications for
ocean initialization. Part I: The ocean data assimilation system.
J. Climate 126, 1013-1021.
-
Cohn, S. E. & Todling, R. (1996):
-
Approximate data assimilation schemes for stable and unstable
dynamics.
J. Meteor. Soc. Japan 74, 63-75.
-
Derber, J. & Rosati, A. (1989):
-
A global oceanic data assimilation system.
J. Phys. Oceanogr. 9, 1333-1347.
-
Hamill, T. M. & Snyder, C. (2000):
-
A hybrid ensemble Kalman filter/ 3D-variational analysis scheme.
Mon. Wea. Rev. , in press.
-
Tippett, M. K., Cohn, S. E., Todling, R. & Marchesin, D.
(2000):
-
Low-dimensional representation of error covariance.
Tellus , in press.
This document was generated using the
LaTeX2HTML translator Version 99.2beta8 (1.42)
Copyright © 1993, 1994, 1995, 1996,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999,
Ross Moore,
Mathematics Department, Macquarie University, Sydney.
The command line arguments were:
latex2html -image_type gif -transparent -no_math -html_version 3.2,math -address -split 0 -local_icons -no_navigation clivar
The translation was initiated by on 2000-10-17
Footnotes
- ... Tippett1
- International
Research Institute for climate prediction, Lamont-Doherty Earth
Observatory of Columbia University, Palisades, NY 10964-8000.
- ... Ji2
- CMB, NCEP, Camp Springs, MD.
- ...
Kaplan3
- Lamont-Doherty Earth Observatory of Columbia
University, Palisades, NY.